Tableau de variation – Performance Scolaire

La construction d’un tableau de variations est une étape fondamentale dans l’étude des fonctions en mathématiques, car il résume la croissance et la décroissance de la fonction, ainsi que ses extremums (maximums et minimums). Le tableau est principalement basé sur l’étude du signe de la dérivée de la fonction.

5️⃣ Étapes pour construire un Tableau de Variations Voici la méthode standard, appliquée aux fonctions dérivables : Étape 1 : Déterminer le Domaine de Définition ( $D_f$ ) Identifiez l’ensemble des valeurs de $x$ pour lesquelles la fonction $f(x)$ est définie. Notez les éventuelles valeurs interdites (par exemple, les valeurs qui annulent un dénominateur ou celles qui rendent un terme sous une racine carrée négatif). Ces valeurs seront marquées par une double barre dans le tableau. Étape 2 : Calculer la Dérivée ( $f'(x)$ ) Utilisez les règles de dérivation pour calculer l’expression de la fonction dérivée $f'(x)$ . C’est le signe de cette dérivée qui vous donnera les variations de la fonction d’origine $f$ . Étape 3 : Trouver les Points Critiques Résolvez l’équation $f'(x) = 0$ . Les solutions de cette équation sont les points critiques (ou extrémums potentiels) où la fonction change de sens de variation (passage de croissance à décroissance ou inversement). Placez ces valeurs, ainsi que les bornes de $D_f$ et les valeurs interdites, sur la première ligne ( $x$ ) de votre tableau, par ordre croissant. Étape 4 : Étudier le Signe de la Dérivée ( $f'(x)$ ) Créez un tableau de signes pour la dérivée $f'(x)$ sur les intervalles définis par les points critiques. Placez un $0$ dans la ligne $f'(x)$ sous chaque point critique. Placez une double barre sous les valeurs interdites. 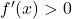Règle fondamentale : Si $\text{[math]}$ 0 » title= »Rendered by QuickLaTeX.com » height= »19″ width= »72″ style= »vertical-align: -5px; »/> (positif) sur un intervalle, alors $f$ est croissante sur cet intervalle. Si <img src="https://eric-limelette.ovh/wp-content/ql-cache/quicklatex.com-c9e0dd405dae040ff2f36c7c70726384_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="f'(x) (négatif) sur un intervalle, alors $f$ est décroissante sur cet intervalle. Étape 5 : Compléter le Tableau de Variations ( $f(x)$ ) Utilisez les signes de $f'(x)$ pour dessiner les flèches dans la dernière ligne ( $f(x)$ ). Une flèche qui monte (↗) pour un signe positif. Une flèche qui descend (↘) pour un signe négatif. Calculer les valeurs : Calculez les valeurs de la fonction $f(x)$ d’origine aux points critiques et aux bornes de l’ensemble de définition (limites).

Shutterstock Explorer

Les valeurs aux pointes des flèches correspondent aux extremums locaux (maximums ou minimums).

🖼️ Structure du Tableau Le tableau est généralement structuré en trois lignes principales : Ligne Description Contenu

$x$

Variable Les bornes de $D_f$ , les valeurs interdites (double barre) et les points critiques ( $f'(x)=0$ ), classés.

$f'(x)$

Signe de la dérivée Les signes (+ ou -) sur chaque intervalle et les $0$ aux points critiques.

$f(x)$

Variations de la fonction Flèches (↗ pour croissant, ↘ pour décroissant) et valeurs (images ou limites) aux bornes et aux extremums.

Si vous souhaitez voir cette méthode appliquée à un exemple concret de fonction, vous pouvez regarder cette vidéo. Comment faire un TABLEAU de VARIATION ? — Maths — Terminale